積分とは
関数y=f(x)とx軸で囲まれた領域の面積。xの範囲が指定されている積分を定積分という。
不定積分の公式の例
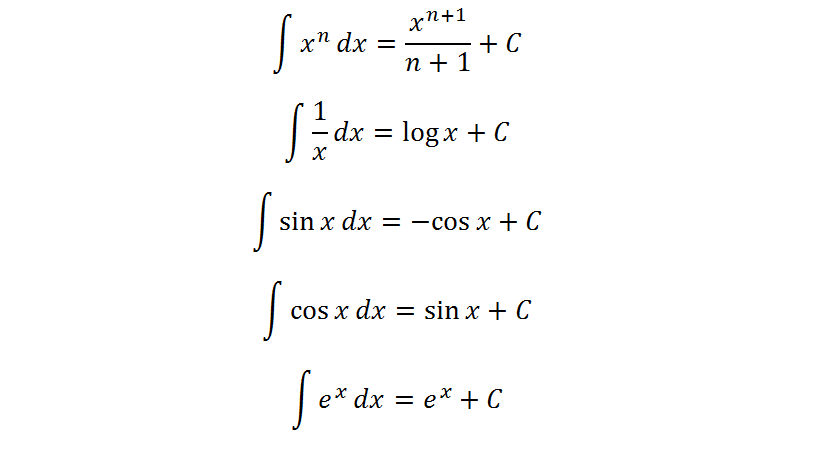
これらの積分は初等関数(n次関数、三角関数、指数関数、対数関数など)で表すことができる。
定積分の例
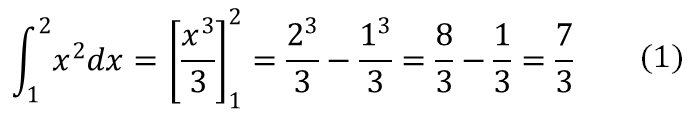
この定積分は簡単に解くことができる。しかし次の定積分を見てほしい。
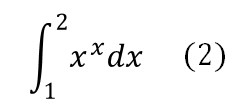
この関数は初等関数の範囲では積分できないため、この定積分の値は数値的に求める必要がある。
数値的に定積分の値を求めることを数値積分という。
数値積分
数値積分の例として、シンプルな方法である区分求積法と台形則を説明する。
上記のように積分とは関数y=f(x)とx軸に囲まれた領域の面積である。xがaからbまでの範囲で積分する場合、積分区間[a,b]と表記する。
この領域を有限個の図形に分割し、それらの図形の面積を合計することで定積分の値が求められる。
区分求積法では長方形に分割する。長方形の面積の求め方は縦×横である。aからbまでをn等分すると、その個々の長さはdx=(b-a)/nとなり、これが横となる。
縦は、n個に分割したk番目のxのときのf(xk)の値となる。すなわちこの方法で定積分を求めると以下のようになる。
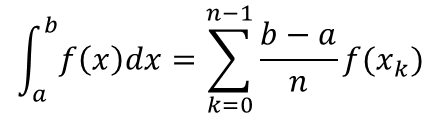
台形則では台形に分割する。台形の面積の求め方は(上底+下底)×高さ÷2である。同様にaからbまでをn等分すると、その個々の長さはdx=(b-a)/nとなり、これが高さとなる。
上底および下底は、n個に分割したk番目および(k+1)番目のxのときのf(xk)、f(x(k+1))の値となる。すなわちこの方法で定積分を求めると以下のようになる。
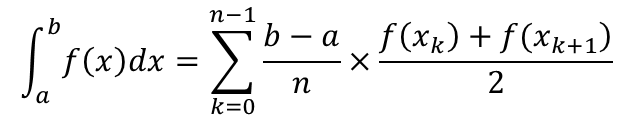
区分求積法よりも台形則の方が誤差が小さい。
コードと結果


出力結果より、区分求積法では2.035...、台形則では2.050...となることが分かった。